2017年05月17日
No.10000149
No.10000149
社会人のためのデータ分析入門 第5回
2変数の類似度合を表す「相関係数」②
前回に続き、各都道府県について調べた2つのデータで散布図を作ってみます。
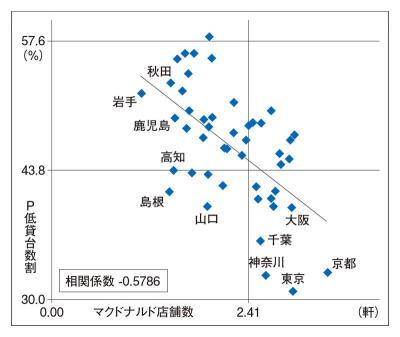
人口当たりのマクドナルド店舗数とパチンコ低貸台数割合には、相関があるでしょうか。パチンコ低貸台数割合は、週刊アミューズメントジャパン2015年8月10日号に掲載されたもので、15年6月末時点のP‐WORLD登録店舗情報をもとにピーワールドインサイトが集計したものです。
散布図を見ると、マクドナルド店舗数が多い都道府県はパチンコ低貸台数割合が低いという傾向が見えます。このように、一方が高いと他方は低い傾向が見られるとき、2つの変数には「負の相関がある」と言います。相関係数はマイナス0.5786で、「中程度の負の相関がある」と言われるレベルです。
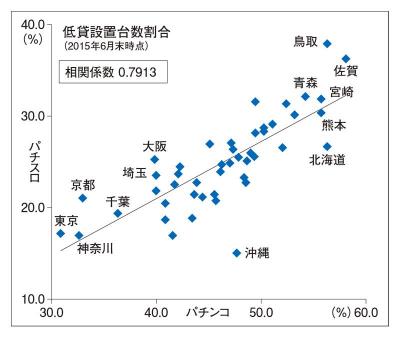
ちなみに、パチンコの低貸台数割合とパチスロの低貸台数割合は下の図ように「強い正の相関がある」と言われるレベルです。
注意していただきたいのは、これらの散布図が意味するのは、「Aが多い都道府県はBも多い。反対に、Aが少ない都道府県はBも少ない」ということであって、因果関係を示してはいません。
常識的に考えても、マクドナルドの店舗数の増減がフェイスブックユーザー数(前回参照)やパチンコ低貸し台数割合に影響を与えているとは思えません。
相関関係は何に役立つかというと、予測です。Aという指標とBという指標(変数)に相関があるという規則性を知っていたら、いずれかの値が分かるともう一方の値の予測ができるのです。ある県のパチンコの低貸台数割合が分かれば、パチスロ低貸台数割合の予測精度が高まるのです。
ファイナンスの分野では、分散投資に利用されています。分散投資とは、資産を複数の対象に投資することで、そのうちの一つが値下がりしたときに、他のものでカバーをしてリスクを回避する方法です。
2つの投資対象の値動きの相関係数が1に近い場合、同時に値下がりしてしまう可能性が高いため、相関係数がマイナスになる、すなわち逆の値動きをすると予測できる投資対象を組み込むのです。
(田中剛・アミューズメントジャパン編集部)
=========
■社会人のためのデータ分析入門 第4回(2017/04/26)
2変数の類似度合を表す「相関係数」①
■社会人のためのデータ分析入門 第3回(2017/04/17)
データのバラツキを表す指標「標準偏差」
■社会人のためのデータ分析入門 第2回(2017/04/07)
データの「分布」確認はなぜ必要なのか?
■社会人のためのデータ分析入門 第1回(2017/03/19)
集計データを代表する平均値・中央値・最頻値